目次
算数の考える力を育てるには、身に付けた知識を使うことが一番
小学5年生の算数の授業で扱う図形は平面図形と立体図形になります。
平面図形では4年生で学習した正方形・長方形・平行四辺形・台形・ひし形に加え、円についても学習します。
算数の授業では一つずつ公式を確認していくのですが、私はいつも「どうしてこの公式なの?」ということを子どもたちに聞くようにしています。
面積の求め方を一緒に考えてみよう
子どもたちに台形の面積の求め方を覚えてるか聞いてみたところ、みんな呪文のようにスラスラと答えてくれました。ちなみに台形の面積を求める公式は「(上底+下底)×高さ÷2」です。
そこで、子どもたちに「台形の面積の公式って何でこの公式なの?」と聞いてみました。
子:「どうゆうこと?」
子:「だってそうやって習ったよ?」
子:「知らなーい!」
ここを考えると「なるほど!」「あぁ!そっか!」という発見があり、学ぶことや考えることが面白くなります。
そこで、台形の面積の公式についてみんなで考えてみることにしました。
私:「じゃぁさ、三角形の面積は何で÷2をするんだっけ?」
子:「四角形の半分だから!」
私:「そうだね。じゃぁ平行四辺形は?」
子:「はい!はいっ!前に習った!
右側を切って、左にくっつけるんだよ!そうすると長方形になるの!」
三角形の面積の求め方までは順調に答えられてノリノリの子どもたち。平行四辺形やひし形の面積の求め方についても同じように答えてくれました。
そしていよいよ台形の面積の求め方です。
私:「大正解!!じゃぁ台形は?」
子:「はい!平行四辺形と一緒!右側を切って、左にくっつけると長方形になるの!」
私:「跳び箱みたいな形の台形だったらそうなるね。でも、こんな形の台形もあるよ?」
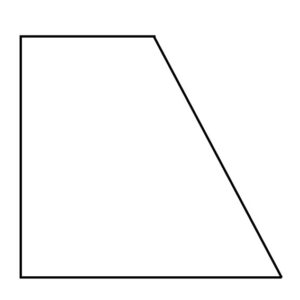
子:「あ、これだと右端切っても左にくっつけられないじゃん!」
子:「えー、なんで?じゃぁどうすればいいのー?!」
子:「横にスパッと切る!」
子:「真ん中で縦に切る!」
子:「ダメだよー!それじゃあ求められない!」
子:「じゃぁ、斜めは?!」
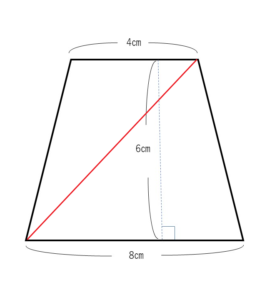
子:「あっ!これなら三角形2つ分じゃん!」
私:「そうだね。じゃぁ2つの三角形の式を書いてみようか」
2つの三角形の面積の式は、「4×6÷2」と「8×6÷2」です。この2つをたせば、台形の面積を求めることができます。ここで台形の面積を求める公式と比べてみると新たにわかることがあります。
私:「2つの式をよーく見て。計算の工夫はできないかな?」
子:「あっ・・・できる!分配法則だ!」
子:「あ!台形の面積を求める式になった!すごーい!」
算数は学んだ知識を使うことを意識することで考える力が身につく
分配方式を使って2つの三角形の式をまとめると「(4+8)×6÷2」という式になります。
分配法則は小学4年生で四則混合計算を学習したときに学習した内容です。
また、三角形や平行四辺形・ひし形の面積の公式を学んだときの考え方をヒントにして、台形の面積の求め方を考えることができました。
私が授業中に、子どもたちによく言っていることがあります。それは「今までに習ったことは使っていいんだよ」ということです。
しかし、子ども達は問題を解いている時に、”習った知識を使っているんだ”と実感しながら問題を解いているわけではありません。
ですから、時々こんな風に、習った知識を使うことで、式の成り立ちを説明できたり、難しい問題が解けたりするということを、子どもたちが実感できるようにしています。
そして、この時の子どもたちの『あっ!!』というヒラメキを、次の学びに繋げていくのです。
しかし、学んだ知識を使うためには情報を整理する力が必要です。
いくら知識を身に付けても、頭の中に入れるだけの詰込み型では、学んだ知識を上手に使えません。算数の情報を整理する方法の一つが単元名です。他にも、計算の手順や図形の特徴をまとめることなども情報の整理になります。
そして、情報の整理が上手くできるようになることは、難しい問題を解くときに必要な応用力にも繋がります。
問題文に書かれている情報を整理しながら、これまでに学習した知識の中から、問題を解くために必要な情報を選ぶことを繰り返すことで、難しい問題を解くことができるのです。
この情報の整理の仕方は整理収納のスキルを学ぶことで身に付けることができます。
生活環境を整え、子どもの考える力を育てることで、自立を促すことができる整理収納教育を、家庭や学校でも子ども達に教えていけたら、それは子どもの生きる力に繋がるのです。



コメント